- Home
- Integers
- Order of Operations
- Sample Quiz
- Pythagorean theorem
- Sample Quiz
- Ratios and Proportions
- Sample Quiz
- Trigonometric Ratios
- Sample Quiz
- Algebra
- Sample Quiz
- Linear Equations
- Sample Quiz
- Linear Systems
- Sample Quiz
- Quadratics Functions
- Sample Quiz
- Multiplying Polynomials
- Sample Quiz
- Factoring
- Sample Quiz
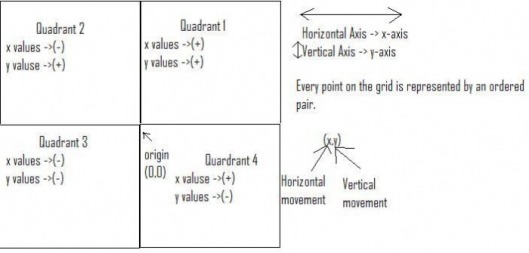
Parts of A Coordinate Grid
Liner Relation
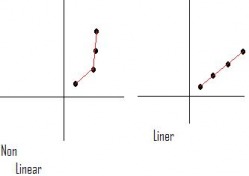
When plotted points on a coordinate grid form a straight line, it is called a LINEAR RELATION.
Ordered Pairs & Table of Values
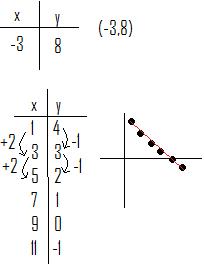
· Find a relationship in the table of values.
· Then find three more co-ordinates.
· Plot it and determine if its linear.
Liner Relation –-Solving Graphically
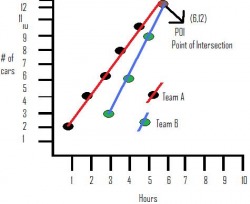
For a car wash fundraiser Team A washes 2 cats per hours, starting at 7:00am. Team B begins washing cars at 9:00 am and washes 3 cars per hours.
Graph the car washing progress of each team.
POI tells us –It is when both teams have the same number of cars washed.
Definition
Linear System – when you consider or look at two or more linear eq’ns at the
same time.
POI = Pont of Intersections – When the two line intercept /cross on the graph it is the co-ordinates found on both lines.
Graphing with a Point and a Slope
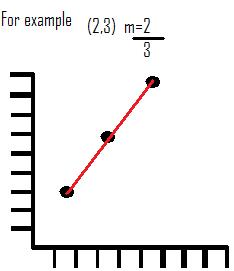
The way you make a graph with a slope and a point is, first you plot the point and then you just add the slop.
m= slop= rise
run
Standard Form Equation of A line
y = mx + b à slope intercept form
Ax + Bx + C = 0 à standard form
We know that we only need minimum of 2 points to draw a line
Example: 2x + 4y +8 = 0
· Find 2 ponits so that you can draw the line.
· The easiest point to choose are the x-intercept and the y-intercept.
y–intercept x–intercept
Lets find the y intercept first. Lets find the x–intercept next.
The x-coordinate for my y-intercept The y–coordinate for my x–coordinate
is zero. will Always be 0.
Substatute zero into the eq’n whenever Substatute zero into the eq’n whenever
you see x. you see y.
2(0) + 4y + 8 = 0 2x + 4(0) + 8 = 0
4y + 8 – 8 = 0 – 8 2x + 8 – 8 = 0 – 8
4y = –8 . 2x = –8 .
4 . . the y–intercept is (0,–2) 2 . . the y–intercept is (0,–2)
y = –2 x = – 4
Rearranging EQ’NS From One Form to Another.
Ex. y = 3x + 1 àput it into standard form Ex. x – 3y + 9 = 0 à put into slop form
Ax + Bx + C = 0 y = mx + b
y = 3x + 1 x – 3y + 9 – 9 + 0 – 9
y – 3x – 1 = 3x – 3x + 1 – 1 x – x – 3y = –9 – x
y – 3x – 1 = 0 –3y = –9 – x
–3x + y – 1 = 0 –3
y = 3 + 1x
A = –3 3
B = 1 y = 1x + 3
C = –1 3