- Home
- Integers
- Order of Operations
- Sample Quiz
- Pythagorean theorem
- Sample Quiz
- Ratios and Proportions
- Sample Quiz
- Trigonometric Ratios
- Sample Quiz
- Algebra
- Sample Quiz
- Linear Equations
- Sample Quiz
- Linear Systems
- Sample Quiz
- Quadratics Functions
- Sample Quiz
- Multiplying Polynomials
- Sample Quiz
- Factoring
- Sample Quiz
Graphing using A Table of Values
The x- values are called the Independent value. This is because the x values comes first and can be whatever you want.
The y-values are called the Dependent values. This is because the y-values “depend” on whatever you chose for x.
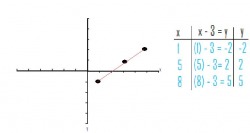
Make a table of values and sketch the graph for line with the equation:
y = x -3
Determine if the point A(2,–3) is on the line with the equation.
y = 2x – 5 x y
L.S R.S L.S R.S .
= y =2x – 5 . . point A is on the line.
=–1 =2(2) – 5
L.S=R.S =4 – 5
= –1
Solving by Substitution
How does substitution works?
Sue baked a cake. Then LindaàSubstitute carol Carol baked a cake. Then Linda
ate that cake that Sue baked.àwher you see Sue ate that cake that Carol baked.
When do you use substitution?
You use this method whenever one or both eq’ns appears in the y =mx + b form.
Example.
Solve the linear system.
y = 3x + 4 (1)ßthis means eq’n #1
2x + y = 9 (2)
Step 1Sub (1) into (2) Step 2 Solve for x Step 3 Sub the value of x
This means replace + 3x + 4 = 9 into eq’n 1 to get the
“y” in eq’n (2) 5x + 4 – 4 = 9 – 4 y value.
with the right side 5x = 5 y = 3x + 4
of eq’n (1) 5 y = 3(1) + 4
x = 1 y = 3 + 4
y = 7
Step 4 Do a check
y = 3x + 4 2x + y = 9 .
L.S R.S L.S R.S Step 5 . . my POI is (1,7).
= y = 3(1) + 4 = 2x + y = 9
= (7) = 3 + 4 = 2(1) + (7)
L.s=R.S = 7 = 2 + 7 L.S=R.S
= 9
Solving by Elimination
What is elimination?
In this method, we add or subtract the eq’n to eliminate (remove) one of the variable.
When do we use elimination?
When both eqa’ns are in standard form, or something similar to it.
Example 1
Solve the linear system.
2x + 5y = 17 (1)
4x – 5y = –11 (2)
Step1 Check to see whether one of the variables can be eliminated by simply .
adding or subtracting the eq’n.
*if sings are different you add them**if the sings are same you subtract*
Step 2 Add or subtract the equation.
2x + 5y = 17
+4x – 5y = 11
6x = 6
Step 3 Solve for variable
6x = 6
6
x = 6
Step 4 Sub x-value into (2)
4(1) – 5y = 11
4 – 4 – 5y = 11 – 4
– 5y = –15
– 5
y = 3
Step 5 Do a check
2x + 5y = 17 4x + 5y = 11
L.S R.S L.S R.S
=2x + 5y =17 =4x – 5y =–11
=2(1) + 5(3) =4(1) – 5(3)
=2 + 15 L.S=R.S =4 – 15 L.S=R.S
=17 =–11
Step 6 There for statement.
.
. . since L.S=R.S for both eq’ns the POI is (1,3)
Example 2
Solve the linear system
x + y = –1 (1)
3x – 4y = 25 (2)
Step 1 In this case, neither adding nor subtracting will eliminate a variable, since
none of the coefficient (the number in front of the letter) are the same.
(1) x 4
4x + 4y = –4 new (1)
Step 2 4x + 4y = –4 (1)
+ 3x – 4y = 25
7x = 21
Step 3 7x = 21 – solve for x
7
x = 3
Step 4 Sub x–value into (1)
(3) + y = –1
3 – 3 + y = –1 – 3
y = –1 – 3
y = –4
Step 5 Do a check.
x + y = –1 3x – 4y = 25 4x + 4y = –4
L.S R.S L.S R.S L.S R.S
= x + y = –1 = 3x – 4y = 25 = 4x + y = -4
= 3 + –4 = 3(3) – 4(–4) = 4(3) + 4(–4)
= –1 L.S=R.S = 9 + 16 L.S=R.S = 12 + –6 L.S=R.S
= 25 = -4
.
Step 6 . . Statement
.
. . your POI is (3,–4)
