- Home
- Integers
- Order of Operations
- Sample Quiz
- Pythagorean theorem
- Sample Quiz
- Ratios and Proportions
- Sample Quiz
- Trigonometric Ratios
- Sample Quiz
- Algebra
- Sample Quiz
- Linear Equations
- Sample Quiz
- Linear Systems
- Sample Quiz
- Quadratics Functions
- Sample Quiz
- Multiplying Polynomials
- Sample Quiz
- Factoring
- Sample Quiz
How do we identify them?
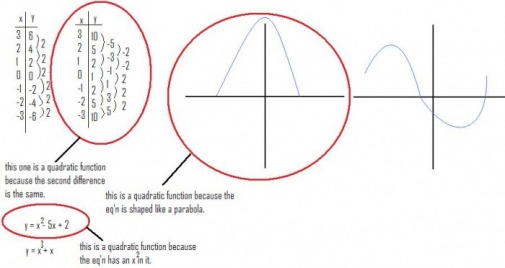
· The second difference is the same
· The graph is in the shape of a parabola/ a U.
· The eq’n has an x2 value.
Everything you need to know about parabolas.
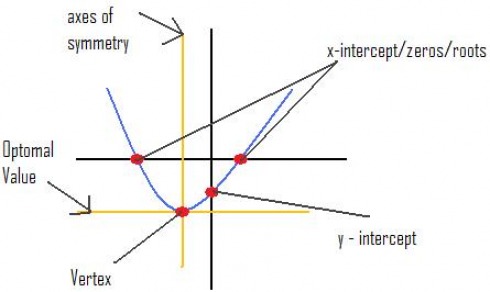
· Parabolas can open up or down.
· The zero of a parabola is where the graph crosses the x–axis.
· Zero can also be called roots or x-intercept.
· The axis of symmetry divides the parabola into 2 equal halves.
· The y-intercept of a parabola is where the graph crosses the y-axis.
· The optimal value is where the graph is at its maximum or minimum.
· The vertex is the point where the axis of symmetry and optimal value cross.
How parabolas move.
Vertical movement
· y = x2 + 3 à Translates up 3 units
· y = x2 – 3 à Translates down 3 units
Vertex movment
· +k à when k is positive the movment is up
· –k à when k is negative the movment is down
Horizontal movment
· y = (x + 3)2 à translates 3 units left
· y = (x – 3)2 à translates 3 units right
Compression/Stretch
· y = 1x2 à vertically compressed by a factor of 1
2 2
· y = 2x2 à vertically stretched by a factor if 2
Reflection
· y =– x2 à reflected in the x – axis
· when a is positive, it opens upwords.
· When a is negative, it opens downwards.
y = a(x – h)2 + k
k
(+) up
(-) down
h
(+) right
(-) left
a
(+) opens up
(-) opens down
(whole #) stretched
(faction) compressed
Moving Quadratics
When a basketball is trown upward, it’s path can be modelled by the function:
y = –4.5(x – 0.1u)2 + 4
When u is velocity(speed)
x is time
y is the height
a. What is the eq’n when the ball is thrown with a velocity of 12m/s?
· sub 12 into u
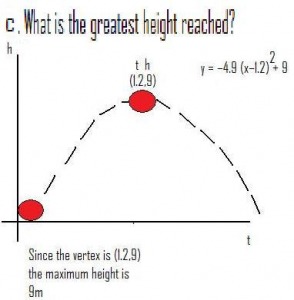
y = –4.9 (x – 0.1(12))2 + 9
y = –4.9 (x – 1.2)2 + 9
b. How many seconds after it is thrown does the ball reach the highest point?
Since the vertex is (1.2,9) we know that it reaches the maximum height of 1.2s.